DIY Geoengineering, Part II
An elementary math error, and the return of the long-lost son of Backyard Hydrogen Generator
My apologies for the delay; I’ve been busy coding. (Startup previews at the end of the post!)
It was brought to my attention during an email exchange a week or two ago that I made an elementary math error in DIY Geoengineering, of the sort that should be embarrassing to a high-school physics student but is, in my defense, not entirely unknown in graduate-level social-science papers—though, as far as I know, is still quite rare in peer-reviewed natural science publications. Here is the detail in which the devil lurks:
One kilo of hydrogen can lift about 1.2 kilos of payload.
That was based on my misreading of Eli Dourado’s Bring Back Hydrogen Lifting Gas! In point of fact, it isn’t a kilo of H2 that will lift 1.2 kilos of payload, but rather one cubic meter. And this makes a serious difference to the numbers.
Assume, again, that we need to lift 500 kilotons of CaCO₃ yearly. Let’s assume we’re clever at designing the spraying apparatus—which is beyond the remit of this blog post and will require some wildcat experimentation, since Harvard's cancelled the SCoPeX experiment after coming under pressure from various NGOs—and only 20% of the payload mass needs to be equipment rather than payload proper. Then we’ll need enough hydrogen to lift 625 kilotons yearly.
At sea level and 25°C (we’re in the tropics, remember), one kilo of hydrogen takes up about 13 cubic meters. Per this PDF, you want to leave about a 15% safety gap between how much mass you’re trying to send up and how much you can theoretically lift, so each cubic meter can lift just over a kilo of mass. (We’ll call it a round kilo). We still need to send up about 1.7 kilotons of payload (625 / 365) a day, but we’ll only need about 130 tons of hydrogen day-in-day-out to do it.
We’ll assume, as in Part I, that we’ll need 80 kWh of electricity to produce a kilo of hydrogen at an electrolyzer capex cost of $100 a kilowatt. That’ll mean 80 kWh * 130,000 kilos = 10.4 GWh of electricity a day. If we assume we’re running our electrolyzers for about 10 hours a day, that’s around a gigawatt of electrolyzer—about $100M. Expensive, but you can amortize it on the books (electrolyzers aren’t that fragile).
As for electricity draw, this now drops to somewhere in the high hundred MW to a gigawatt or two depending on how intermittent your power source is. Current wholesale electricity prices are about a dime a kilowatt-hour in moderately cheap markets, so you’d be shelling out about a million dollars a day if you bought the power directly off the grid. If you can borrow at low interest rates, or can just drop a load of cash on the venture without borrowing, you could just build your own power plant. Assuming eight hours a day of sun coverage (we’re in the tropics, remember), we’d need about 1.25 GW of nameplate solar capacity. Utility-scale solar panels are now somewhere around twenty cents a watt, though the cost of the module alone is starting to be outweighed by other costs, like installation and trackers. In a country where construction labor is fairly cheap, you could plausibly get the total cost down to, let’s say, fifty cents a watt—~$600M or so.1
Let’s ditch the silly boats from part I. Agreed. What are our total costs?
We’ll assume we’re amortizing costs over a 20-year period and need to replace a fifth of the solar panels and electrolyzers. Total cost $120M for the electrolyzers and, at most, $720M for the solar panels—probably less in the latter case especially because we can just chuck the repair budget into a Vanguard fund and watch module prices drop over the time period. (I do not get the sense that electrolyzers have a strong learning curve, especially if you’re using simple ones that compensate for their lack of fancy transition metals like platinum by throwing more dakka at the water.)
Since we need only a thirteenth as much hydrogen, there might be no point in trying to recover it. The law of conservation of energy is, of course, inescapable, so you’ll need to work against gravity to get a floating object down, and then some. If the equipment was 20% of the payload (26 kilotons a day) and you sent the whole thing up to 20 kilometers, you’ll need to expend at least 9.8 m/s² * 26,000 kg * 20,000 m = 5.1 gigajoules = 1.4 MWh a day to get the payload and balloon down. This might be worth it at scale, but for now we’ll hand-wave it. (Thanks to C. Handmer for sanity-checking this one.)
If we assume we just let the things pop once they’re up there, we have another conundrum: wouldn’t the water vapor thus produced (after the hydrogen reacts with surrounding oxygen) cause additional warming?2
The short answer is ‘not enough to worry about’. The long answer is that the stratosphere contains about 1.4 gigatons of water vapor. Over the course of a year, we’d be sending about 48 kilotons of hydrogen into the atmosphere—enough to add about 432 kilotons of water vapor over the course of a year. The Hunga Tonga eruption released about 8.9 megatons of H2O, about a 9% increase in total stratospheric water vapor content. The stratosphere is about 2-7 ppm H2O depending on when and where you measure—quite dry, in any case—which means that we’d be contributing somewhere on the order of 0.5% extra H2O on a yearly basis, much of which would precipitate out before long. One part per million of stratospheric H2O contributes about 0.03 W/m² to forcing:
We are now at about 3.5 W/m² of extra forcing, total, from all greenhouse gases. The extra water vapor would cause some warming counteracting the activity of the calcite, but only in the same way that an eighteen-wheeler slows down when it runs over a stick. This is not a serious concern.
Revised total costs?
Total capex costs for the electrolyzers and power supply are just under a billion dollars—$50M a year over twenty years, within the remit of an eccentric tycoon or small Pacific island country.
Opex costs aren’t negligible and, in fact, probably outweigh capex. “Industrial-grade” calcite costs about $120/ton; since we’re being particular about particle size, we’ll call is $250. That’s about $425,000 a day or $155M a year. You might be able to push this down depending on how easy it turns out to be to get the right size distribution; $150M a year for the whole thing might be possible, and it wouldn’t take twenty years to start working (but you’d probably need to launch enough from day 1 for it to make a dent in rising temperatures).
On the other hand, the backyard-hydrogen cowboy approach starts to make sense again. The FAA limits you to a twelve-pound double payload to launch a balloon without a loicence; that’s about 5.45 kilos, requiring about half a kilo of hydrogen, and you could presumably get the right particles and an altimeter-triggered dispenser by mail-order if anybody was selling them. A balloon of this nature would be a sphere about 1.15 meters in diameter—not tiny, exactly, but not gargantuan either.
You could do this with natural gas, but at this scale you might as well do it with propane. This paper gives a decent overview. For half a kilo of hydrogen, you’ll need just over a kilo of propane—about an eighth of a twenty-pound tank’s worth—and a few liters of water. Full conversion is achieved at about 625°C, well more than a standard oven. The literature seems to suggest that the process is most efficient with methane reforming, though it’s unclear. Methane seems to require higher temperatures than propane, but nobody seems to be doing small-scale experiments on this; the propane reactor was able to use atmospheric pressure, albeit with rather pricey catalysts, which suggests that we can probably avoid the risk of the thing exploding if we’re sufficiently careful. Evacuate the air out, flush some propane and water in, and heat it up. And there’s a tradeoff between catalyst efficiency and catalyst price; we might be able to get good enough results just by, say, throwing some nickel foam in. Experimentation is needed!
You’ll get quite a bit of CO2 as a side effect; enough propane-reforming to produce half a kilo of H2 will give you about 3.3 kilos of CO2. The lime cycle requires very high temperatures, so you might be better off using a few kilos of sodium carbonate, which can cycle to and from baking soda at about 120C. There are probably other alternatives available here, but CO2 absorption by sodium carbonate can go fast.
I’ll try to write a quick note in the next day or two if I have it in me to re-run the energy costs (I am all too aware of my laziness here). The point is that this is, indeed, DIY Geoengineering if you have the right equipment—probably just a large-ish steel box-like thing (lined with nickel—it’s a decent catalyst) with a ceramic coat to protect the surroundings from its heat, a propane tank, a large jug of water, a balloon, some calcite dust and a nozzle to spew it out of; SCoPeX’s untimely cancellation makes the case for wildcat experiments on particle delivery even stronger. You heat six or seven kilos of baking soda up on the thing (producing sodium carbonate) and bubble it through a water-and-sodium-carbonate solution—or merely onto the sodium carbonate—for a few minutes to clear the CO2 out, then fill the balloon. Capex costs for a personal unit would probably run a few hundred at scale; the heat required is considerable but probably not unworkable. A few hundred thousand concerned citizens could get us back to preindustrial temperatures in their backyards.
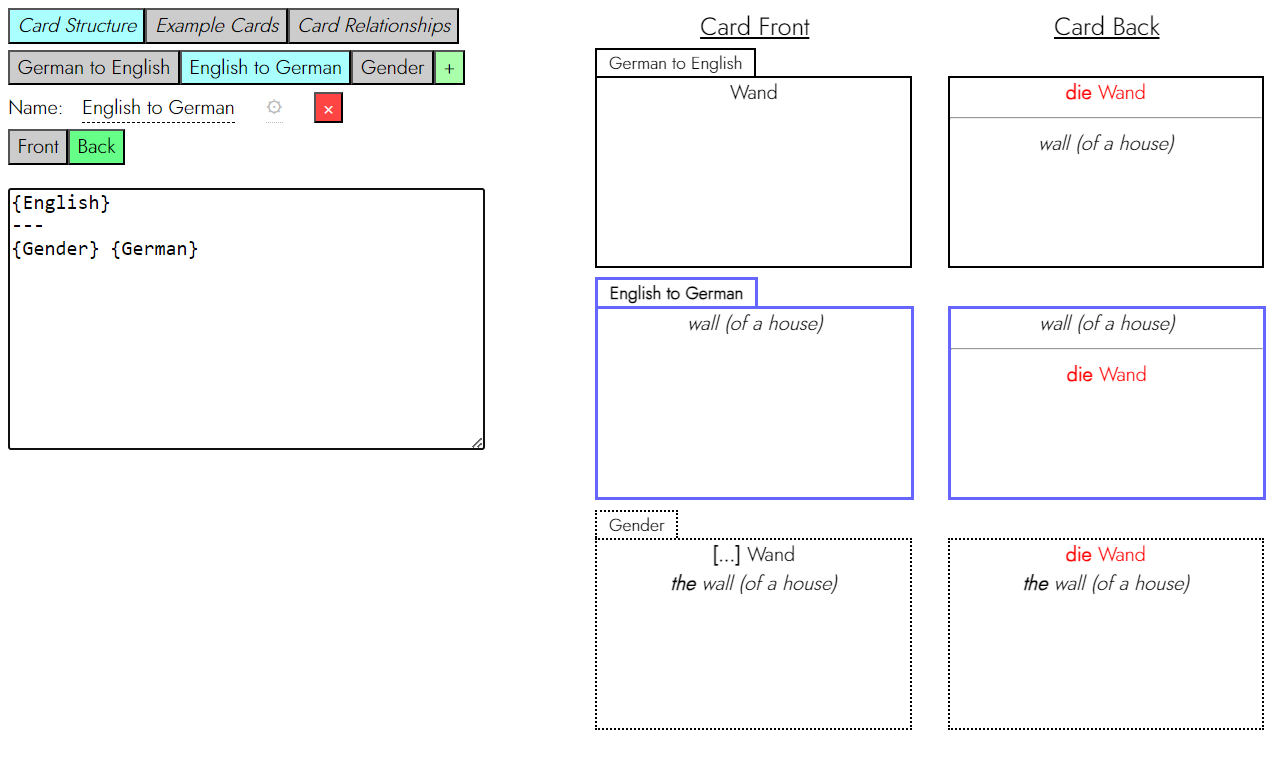
Startup, you had a flashcard startup…
I do indeed. A few previews:
Still planning on having a prototype for individuals out by the end of the summer and possibly even sooner; we’re getting a toy database hooked up this and next week. A reminder that you can donate here (I am forced by GoFundMe not to promise any freebies, but…wink, nudge.)
It still has no name. Get in touch if you can think of one.
If you’re skeptical about this figure, wait a year or two.
To be clear, this is a conundrum I have seen posed primarily by worrywarts on Twitter.




For the startup name, how about:
1) "Mentat" - the human computers from Dune?
2) "Mentate" - a weird word for thinking?